2017 is voorbij en de meeste bedrijven zijn bezig met de jaarafsluiting en het opmaken van de jaarrekening en fiscale aangifte. Het gros doet dit uiteraard conform de (fiscale) wet- en regelgeving, maar er zijn ook bedrijven/personen die de cijfers anders willen doen voorkomen dan de werkelijkheid. Voor deze mensen geldt: vergeet de wet van Benford niet! Iemand die bedrog pleegt en fictieve posten opvoert, slaagt er immers bijna nooit in de cijfers echt willekeurig te verdelen.
De wet van Benford
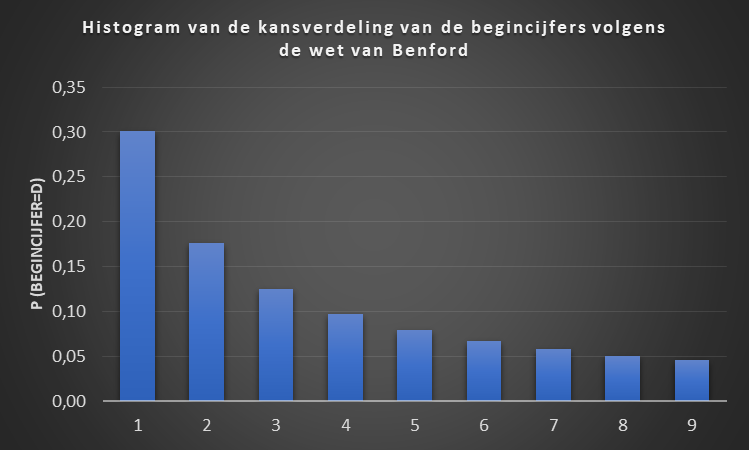
De wet van Benford is vernoemd naar de natuurkundige Frank Benford, die stelt dat de verdeling van de begincijfers van getallen die deel uitmaken van een dataset logaritmisch verdeeld zijn en geen uniforme verdeling volgen. Deze wet maakt het mogelijk om te voorspellen hoe vaak een nummer tussen 1 en 9 voorkomt als eerste nummer in een dataset. Benford toonde aan dat de kans dat in een reeks getallen een getal met een 1 begint, ongeveer 30% is. De kans dat een getal met een 9 begint, is daarentegen slechts 5%.
De wet van Benford kan gebruikt worden om financiële en fiscale data te analyseren. Als de data niet voldoet aan de voorspelling volgens de wet van Benford kan het betekenen dat de data gemanipuleerd is.
Wat kunnen we hier mee?
Vraag eens aan mensen om je heen om honderd willekeurige getallen op te schrijven. Omcirkel van al deze getallen alleen het eerste cijfer. Tel vervolgens hoeveel keer je 1 omcirkeld hebt en doe dit ook voor de andere cijfers van 2 tot en met 9. Je merkt al snel dat alle cijfers ongeveer evenveel voorkomen. Zo kunnen we dus nagaan of getallen willekeurig gekozen worden in plaats van dat ze er met een bepaalde reden staan (zie tevens deze link over een frauduleuze advertentie). Dit is de reden waarom we de wet van Benford kunnen gebruiken in de strijd tegen de misdaad.
Wanneer bepaalde cijfers of cijfercombinaties vaker voorkomen dan verwacht op basis van de wet van Benford, gaan er alarmbellen rinkelen. De wet van Benford is namelijk niet te manipuleren of na te bootsen.
Waar kan de wet van Benford allemaal op worden toegepast?
Helaas voldoen niet alle datasets aan de wet van Benford. Zo geldt bijvoorbeeld dat getallen die gegenereerd zijn aan de hand van een random proces, zoals loterij getallen of dobbelsteenworpen, niet de verdeling volgen volgens de wet van Benford. Financiële en fiscale data voldoet (bij benadering) wel aan de wet van Benford.
De wet van Benford kent vele toepassingen in de praktijk. De belangrijkste toepassing van deze wet bevindt zich op het gebied van fraudedetectie in financiële en fiscale overzichten van bedrijven en door de Belastingdienst bij de fiscale aangiften. Ook wordt de wet toegepast op uitslagen bij verkiezingen.
Ook de woordkeuze is relevant
Potentiële fraude kan ook blijken uit de woordkeuze. Onlangs heeft Marcia Fissette onderzoek gedaan naar de gebruikte woorden in de managementdiscussie die is opgenomen in de jaarrekening (text mining to detect indications of fraud). Via machine learning (een ingewikkeld proces waarbij algoritmes de patronen in teksten kunnen herkennen) heeft de computer een keuze gemaakt of een jaarrekening frauduleus was of niet. Bij de test heeft de computer in 89% van de gevallen het juist gehad.
Men denkt dus dat ze bewust de juiste getallen of woorden kiezen, maar dat is niet zo.